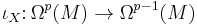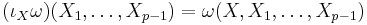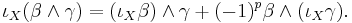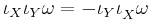Interior product

Not to be confused with Inner product.

In mathematics, the interior product is a degree −1 antiderivation on the exterior algebra of differential forms on a smooth manifold. It is defined to be the contraction of a differential form with a vector field. Thus if X is a vector field on the manifold M, then

$\iota_X\colon \Omega^p(M) \to \Omega^{p-1}(M)$

is the map which sends a p-form ω to the (p−1)-form i_Xω defined by the property that

$( \iota_X\omega )(X_1,\ldots,X_{p-1})=\omega(X,X_1,\ldots,X_{p-1})$

for any vector fields X₁,..., X_p−1.

The interior product, named in opposition to the exterior product, is also called interior or inner multiplication, or the inner derivative or derivation, but should not be confused with an inner product. The interior product ι_X ω is sometimes written as X ⨼ ω; this character is U+2A3C in Unicode and looks like 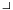$\lrcorner$ .

The interior product is the unique antiderivation of degree −1 on the exterior algebra such that on one-forms α

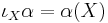$\displaystyle\iota_X \alpha = \alpha(X)$ ,

the duality pairing between α and the vector X. Explicitly, if β is a p-form and γ is a q-form, then

$\iota_X(\beta\wedge\gamma) = (\iota_X\beta)\wedge\gamma%2B(-1)^p\beta\wedge(\iota_X\gamma).$

Properties

By antisymmetry,

$\iota_X \iota_Y \omega = - \iota_Y \iota_X^{ } \omega$

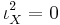and so $\iota_X^2 = 0$ . The interior product relates the exterior derivative and Lie derivative of differential forms by Cartan's identity:

$\mathcal L_X\omega = \mathrm d (\iota_X \omega) %2B \iota_X \mathrm d\omega.$

This identity is important in symplectic geometry: see moment map.

Interior product

Properties

See also